跳转至

968. 监控二叉树

力扣链接(困难)：https://leetcode.cn/problems/binary-tree-cameras

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

img

Text Only
1
2
3
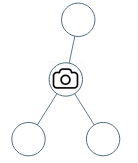
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

img

Text Only
1
2
3
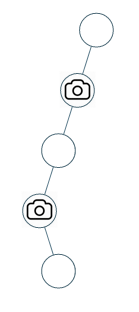
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

  1. 给定树的节点数的范围是 [1, 1000]。
  2. 每个节点的值都是 0。

个人题解

整个遍历逻辑为后续遍历，中节点负责监视左右子节点的情况，每一层递归都需要保证当前节点的子节点被监视，从整体上来看就是全局最优，整颗树被监视。

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 要使得摄像头最少，那么叶子节点一定不能放摄像头
    // 摄像头能监控上下两层，叶子算是最后一层，没有必要放摄像头
    int result = 0;
    /*
    * @return int
    * 0 该节点无覆盖
    * 1 该节点有摄像头
    * 2 该节点有覆盖
    */
    int traversal(TreeNode* node) {
        // 空节点返回有覆盖是为了让叶子节点状态为无覆盖
        // 这样叶子节点的父节点才会安装摄像头
        if(!node) return 2;

        int left = traversal(node->left);
        int right = traversal(node->right);

        // 根据左右儿子返回值，处理其父节点
        // 左右节点都覆盖，则父节点无覆盖
        if(left == 2 && right == 2) return 0;
        // 左右节点至少有一个无覆盖，此时父节点需要加摄像头，保证子节点被覆盖
        if(left == 0 || right == 0) {
            result++;
            return 1;
        }
        // 左右节点至少有一个摄像头，此时父节点不需要摄像头
        if(left == 1 || right == 1) return 2;

        return -1;
    }
    int minCameraCover(TreeNode* root) {
        // 处理根节点未被覆盖的情况
        // 根节点没有上一层，所以需要自监视
        if(traversal(root) == 0) result++;

        return result;
    }
};